The cost of random writes
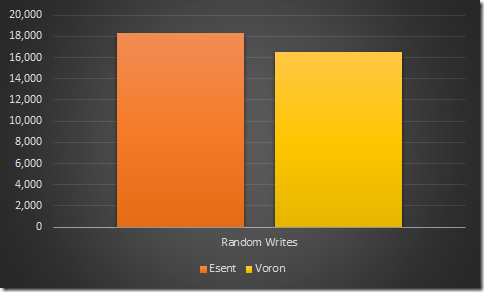
After pretty much getting to where we wanted with sequential writes, it is time to try to tackle the cost of random writes. Here is Esent & Voron doing random writes for 1 million entries:
Yes, it is sad that this is the case, because we can do about 40 times better for sequential writes.
However… what is the reason for the slowness? As usual, the answer is to profile, profile & profile. In fact, we want to do profiling on multiple machines, to check that we don’t have a machine bias.
At any rate, as you can see, we are actually pretty close to Esent in random writes, but why are we so much slower than our performance during sequential writes?
Well, we actually covered that, actually. The major reason for the cost is actually the fact that we have to deal with very different B-Tree shapes. You can see the difference between sequential and randomly inserted trees here. The more random you are, the bigger your tree is, the more pages you have to touch whenever you update. Our scenario calls for making 100 random modification in every transaction. That means that on every transaction, we have to touch many different parts of the tree.
Here are the results (in pages) for how much it cost us (in this test, we run 5,000 transactions of 100 items each.
| Sequential | Random | |
| Average | 7.06 | 111.37 |
| Max | 11.00 | 134.00 |
| Total | 35,320.00 | 556,973.00 |
| Std Dev | 0.35 | 7.09 |
In other words, this means that on average, a sequential transaction wrote 7 pages, or about 28Kb. While the average random transaction wrote about 450Kb!
While the total size written for sequential was 137MB, and allocate 319MB. However, random sizes wrote 2.1 GB for 2.3 GB that were allocated. And that explains quite a lot about the whole thing. (Note that we count for writes only the journal writes, not the data writes, because those are the limiting factor for write performance).
Esent, by the way, writes sequentially about 465 MB and 2.3GB for random writes. Now we know why we are pretty close, because the vast majority of the time is actually spent just writing to the disk, and we are stalled by the sheer amount of data we have.
Interestingly enough, I don’t think that there is a good way to handle that nicely. Certainly not with a B-Tree. We’ll see how we can work with that at a future post.






Comments
When you say sequencial writes, it's about the keys? But sequential keys are wroten sequentially in disk?
Fujiy, We are using a B+Tree structure. The pattern of inserts into the B+Tree is very important. See the link in the post for demonstrating the difference.
For fast inserts, people these days are generally going with a log-structured merge tree, cache-oblivious lookahead array, or something of that sort. B-trees tend to fall over and die on random inserts, while LSMs and COLAs just chug away like nothing's different.
Chris, Those become a lot harder when you are dealing with persistent data. In particular, LSM usually need to do the merging at some point, and that cause write amplification. I've been able to find a persisted COLA impl to look at, though. Do you know of any?
Chris: "people these days" are generally stupid trend-followers. Reality is that LSMs suck in sustained write loads. E.g. http://symas.com/mdb/hyperdex/
Comment preview